Fairness

Once a valid application has been submitted, five reviewers will be assigned to score each submission. These reviewers will offer both scores and comments for each of four distinct traits. Each of the four traits will be scored on a 0-5 point scale, in increments of 0.1. Those scores will combine to produce a total score. Examples of possible scores for a trait are: 0.4, 3.7, 5.0, etc.

The most straightforward way to ensure that everyone is treated by the same set of standards would be to have the same reviewers score every application; unfortunately, due to the number of applications, that is not possible. Since the same reviewers will not score every application, the question of fairness needs to be carefully explained. One reviewer may be a “tough grader”, giving every assigned submission a range of scores only between 1.0 and 2.0; meanwhile, another reviewer may be more generous and score every submission between 4.0 and 5.0. 

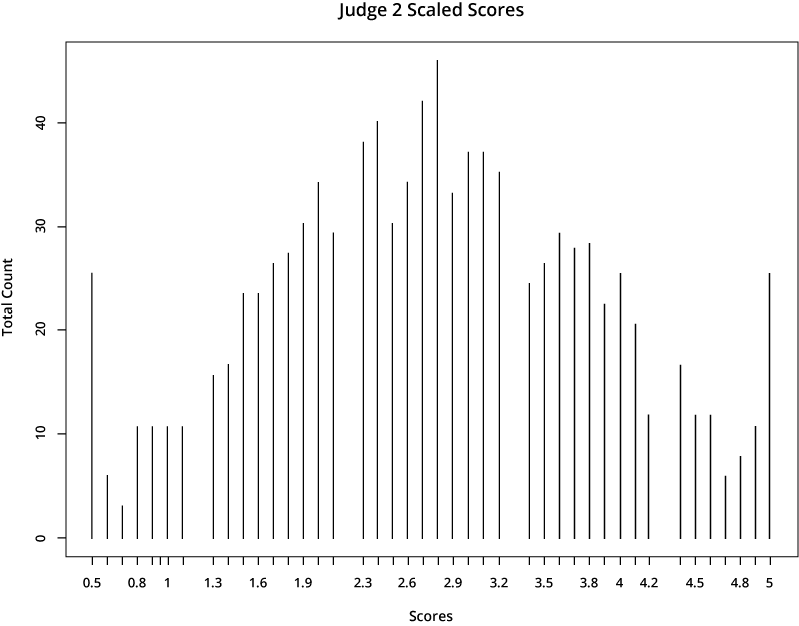
For illustrative purposes, let’s look at the scores from two hypothetical judges:
‍

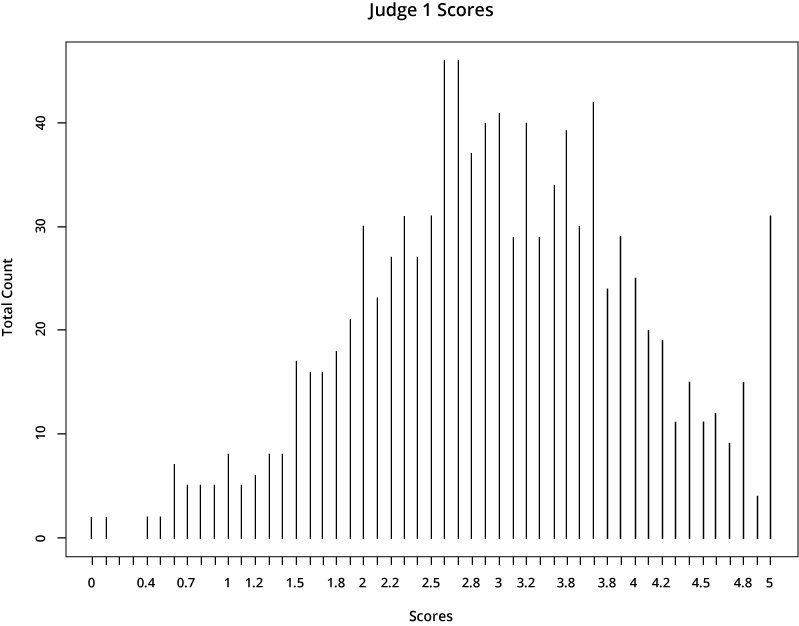
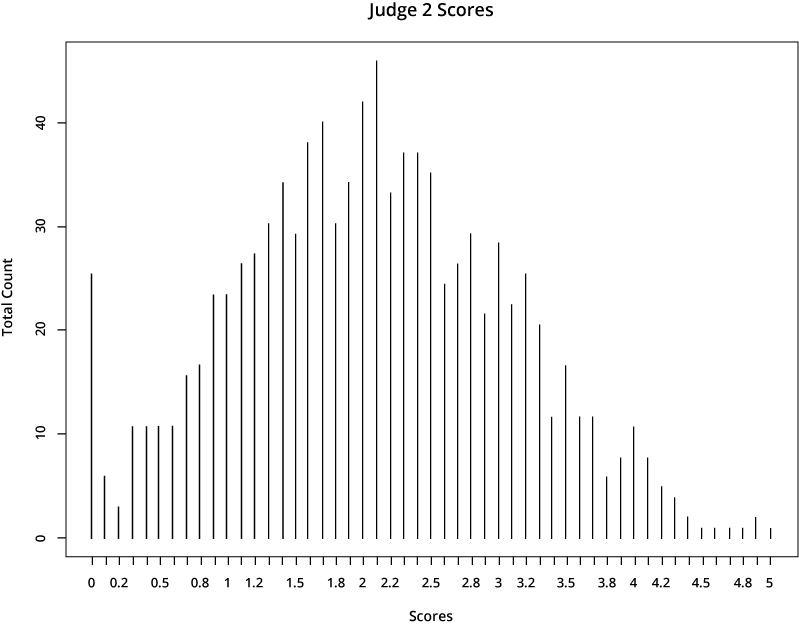
The first reviewer is far more generous in scoring than the second reviewer, who gives much lower scores. If your application was rated by the first reviewer, it would earn a much higher total score than if it was assigned to the second reviewer.

We have a way to address this issue. We ensure that no matter which reviewers are assigned to you, each application will be treated fairly. To do this, we utilize a mathematical technique relying on two measures of distribution, the mean and the standard deviation.

The mean takes all the scores assigned by a reviewer, adds them up, and divides them by the number of scores assigned, giving an average score.

Formally, we denote the mean like this:

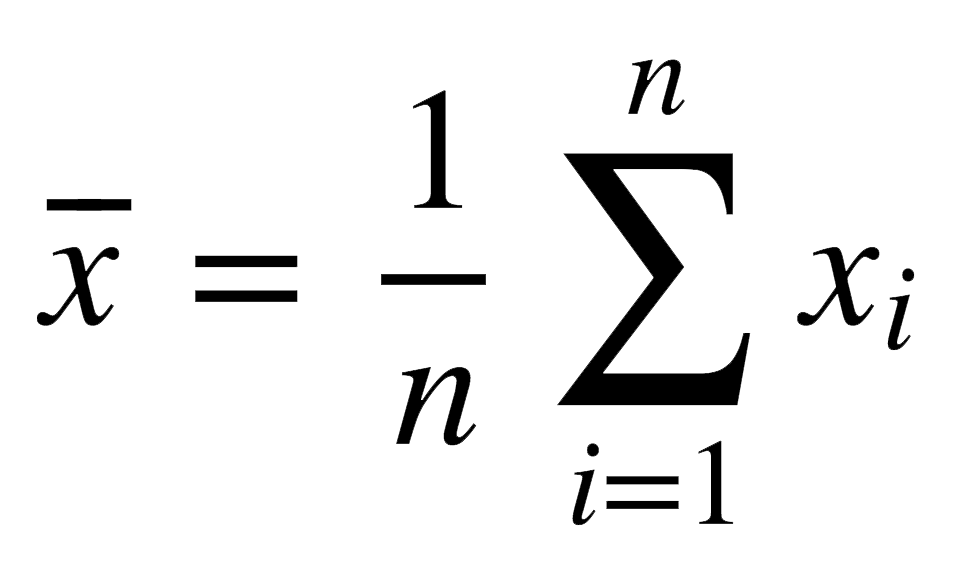
The standard deviation measures the “spread” of a reviewer’s scores. As an example, imagine that two reviewers both give the same mean (average) score, but one gives many zeros and fives, while the other gives more ones and fours. In a competition that seeks to fund the “cream of the crop”, it wouldn't be fair if we didn’t consider this difference.

Formally, we denote the standard deviation like this:

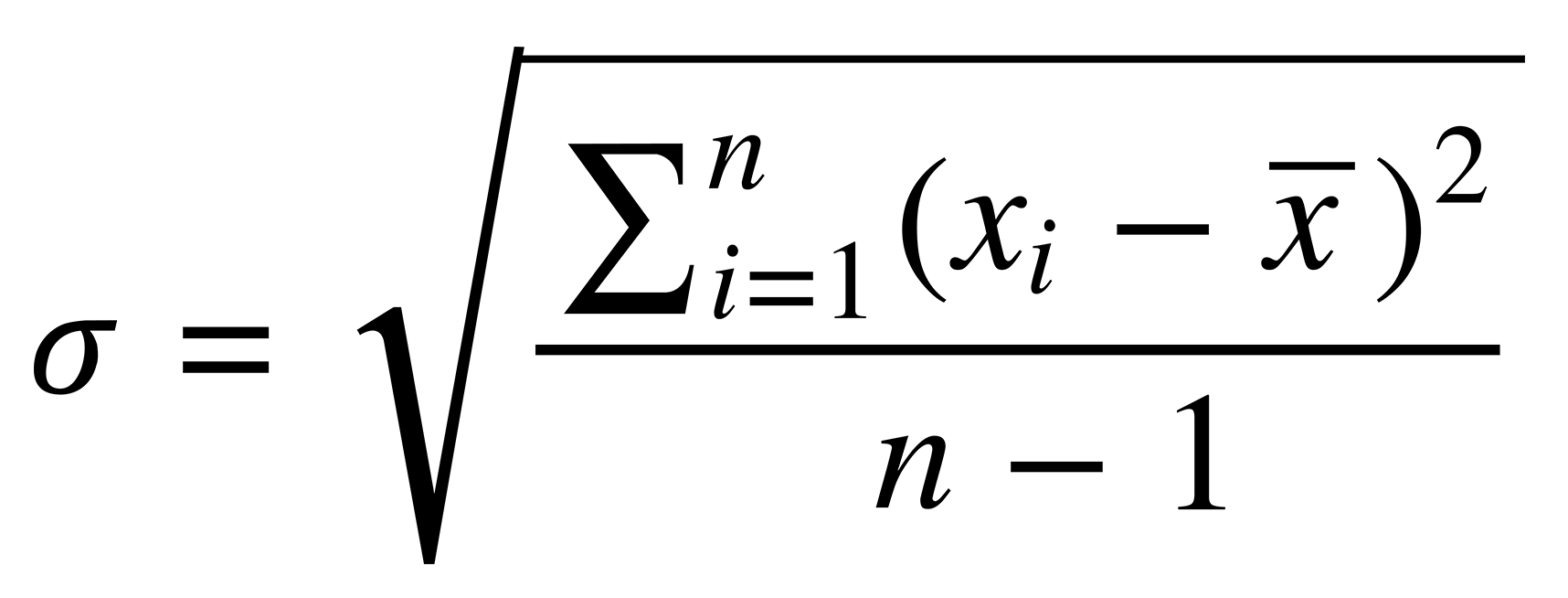
To ensure that the review process is fair, we rescale all the scores to match the reviewing population. In order to do this, we measure the mean and the standard deviation of all scores across all reviewers. Then, we change the mean score and the standard deviation of each reviewer to normalize them across reviewers.

We rescale the standard deviation like this:

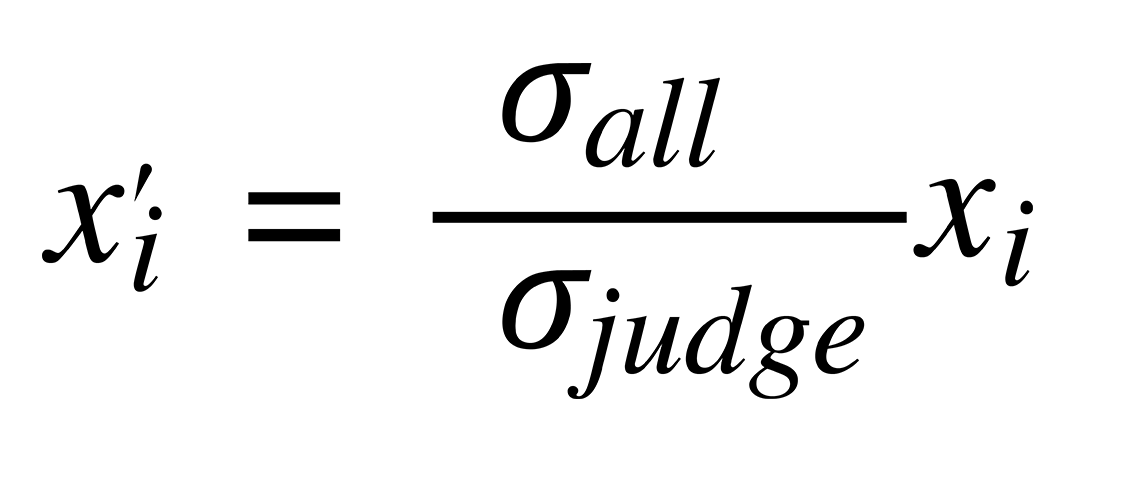
Then, we rescale mean like this:

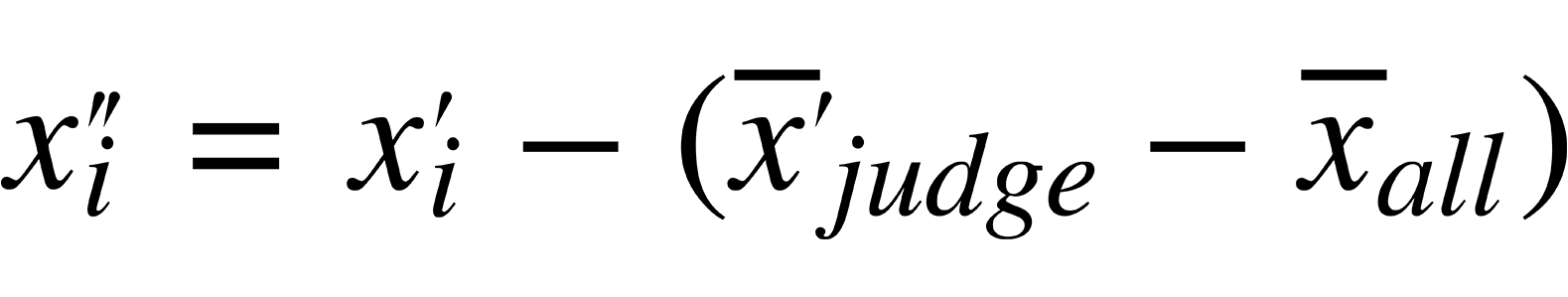
Basically, we are finding the difference between both distributions for a single reviewer and those for all of the reviewers combined, then adjusting each score so that no one is treated unfairly according to which reviewers they are assigned.

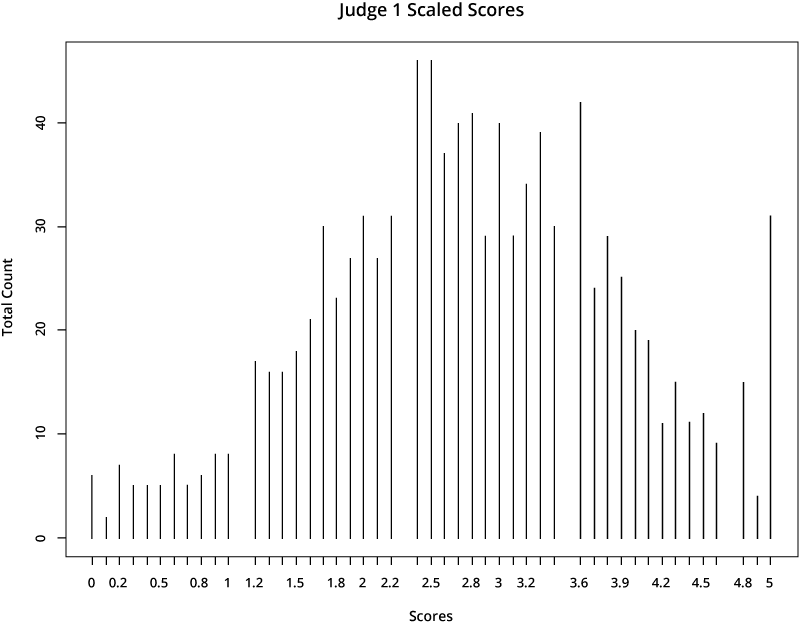
If we apply this rescaling process to the same two reviewers in the example above, we can see the outcome of the final resolved scores. They appear more similar, because they are now aligned with typical distributions across the total reviewing population.

We are pleased to answer any questions you have about the scoring process. You are able to ask questions related to the scoring process on the discussion forums once you register and begin developing your application.